Outline of Hypothesis Testing
Hypothesis testing offers statistical analysis of the data collected by the researcher. let us test our assumptions and beliefs through the use of information evaluation. This manner we will say how probably something is to be true or not within a given normal of accuracy. You may know all of the stats on the planet, but when the incorrect conclusion is improper, you possibly can make a multimillion error. So establishing the suitable Speculation is necessary.
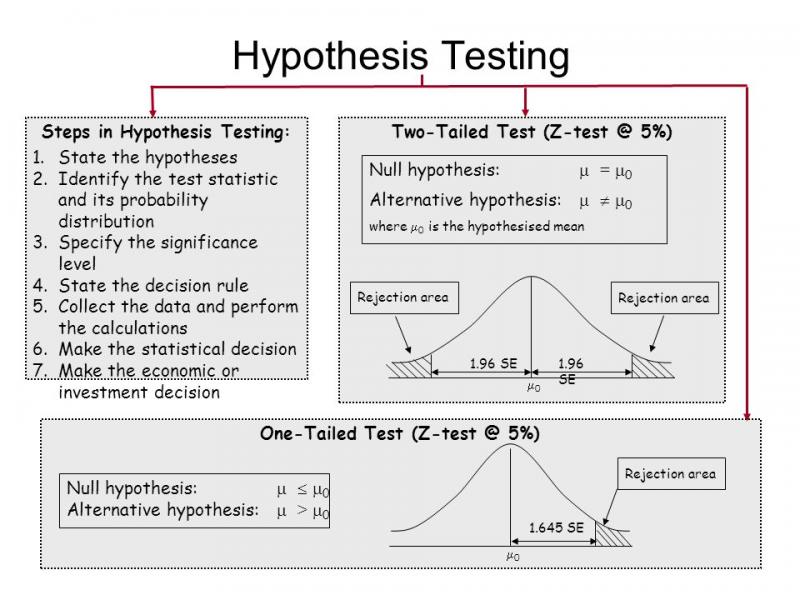
Steps to Hypothesis Testing
- Establish the suitable query to ask.
Ex. Are Cycle instances / Error charges / Conversion charges statistically totally different based mostly on totally different options (teams of individuals, processes followed, geography, level of training, age, and many others)
- Decide the level of significance needed.
How sure will we be of the sampling? Bear in mind; you solely use speculation testing when analyzing a pattern of complete inhabitants.
- Choose the right test for the data.
That is primarily based on the form of knowledge you've got and the sort of query you're asking.
- Interpret the outcomes.
The P worth is integral in utilizing a speculation check to decide. It displays the potential for falsely rejecting the null speculation when it truly is true.
If the P worth is lower than or equal to the agree-upon significance stage (alpha), then you definitely reject the null and might help the alternate speculation.
If the P worth is bigger, you then can not reject the null speculation. (in stats phrases, it's a must to fail to reject the null) And thus you can not help the alternate.
- Make a decision based on these results.
Null Speculation = Assumption that the experimental outcomes are as a consequence of likelihood alone; nothing (from 6M) influenced our outcomes
Alternate Speculation = We anticipate finding sure final result
Important outcomes = When the experimental outcomes should not more likely to occurred by probability
Instance #1: Has cycle time of my transaction has modified from 12 months 1 to 12 months 2
H0 = Average of 12 months 1 = Average of 12 months 2; No change occurred; any change is because of probability alone
Ha, = Average of Yr 1 NOT = Average of Yr 2.
Instance # 2: Decide is a brand new machining course of has decreased the diameter of a product
H0 = It didn't scale back the diameter
HA = It did scale back the diameter
Test statistic
Is calculated from pattern information. To be able to take a look at the null speculation, a check calculation is produced from the pattern. That calculated (take a look at) worth is then evaluated it to an essential worth. Relying on the comparability, choices are made primarily based on the place the take a look at statistic fall primarily based on the crucial worth.
NULL speculation isn't accepted; it fails to reject. We're all the time testing the NULL.
If the TEST STATISTIC falls within the rejection area (past crucial worth), then we REJECT THE NULL
Confidence degree (95%) + Significance stage (5%) = 100 %
As a consequence of likelihood alone 95% of the time the check statistic will fall within the “Fail to reject” area, and 5% of the time as a result of likelihood alone, the check statistic will fall within the “Essential area or Rejection Area.”
P worth: The likelihood of the pattern being studied might have drawn from the inhabitants attributable to probability
- If P is low, Null should Go
- Null Hypothesis ( Hero )
- The assumptions that experimental outcomes are as a consequence of probability alone is known as Null Speculation.
- A Null Speculation is what you'd anticipate by likelihood alone.
- A Null Speculation assumes issues to be equal.
- A Null Speculation is NOT your principle
- When the null speculation accommodates solely an equal signal
- The speculation takes a look at has two tails (or rejection areas).
- The choice speculation accommodates a “not equal to” signal.
- It may be rejected by the check statistic being considerably giant or small.
Statement of zero or no change. If the unique declare contains equality (<=, =, or >=), it's the null speculation. If the unique declare doesn't embody equality (<, not equal, >) then the null speculation is the complement of the unique declare. The null speculation all the time consists of the equal signal. The choice is predicated on the null speculation.
Alternative Speculation ( H1 or Ha )
That is your principle.
An assertion which is true if the null speculation is fake. The kind of take a look at (left, proper, or two-tail) is predicated on the choice speculation.
When the null speculation incorporates solely an equal signal, the choice speculation comprises a “not equal to” signal.
Different Speculation for a Two-Tailed Takes a look at
H0: µnew = µpresent Ha: µnew will not be = µpresent
Errors
Sort 1 Error (Alpha) – Occurs when our significance stage is just too massive
Kind 2 Error (Beta) – Occurs when our significance degree is simply too small
Type I error (alpha risk)
Rejecting the null speculation when it's true (saying false when true). Often the extra critical error.
Sort 1 error includes the Significance degree. For instance, if alpha = 5%, then 5% of the time we are going to say there's an actual distinction between the null and alternate speculation (reject the null speculation) when there isn't a proof of a distinction.
Type II error (beta risk)
Failing to reject the null speculation when it's false (saying true when false).
- alpha
- Chance of committing a Type I error.
- beta
- The probability of committing a Type II error.
- Test statistic
- Pattern statistic used to determine whether or not to reject or fail to reject the null speculation.
- Two-Tailed Test
- H0: µnew = µpresent Ha: µnew shouldn't be = µpresent
For instance, if the null hypothesis has an equal signal, then this can be a two-tailed check, and you need to use the check statistic to reject the null hypothesis if the check statistic is just too massive or too small.
Critical region
Set of all values which might trigger us to reject H0
Important value(s)
The worth(s) which separate the essential area from the non-critical area. The crucial values are decided independently of the pattern statistics.
A crucial worth separates the rejection area from the non-rejection area.
Significance level (alpha)
The likelihood of rejecting the null speculation when it's true. Alpha = zero.05 and alpha = zero.01 are frequent. If no stage of significance is given, use alpha = zero.05. The extent of significance is the complement of the extent of confidence in estimation.
The significance stage (denoted by Alpha) is the chance that the take a look at statistic will fall within the important area when the null speculation is true.
Decision
An announcement primarily based upon the null speculation. It's both “reject the null speculation” and “fail to reject the null speculation.” We'll by no means settle for the null speculation.
Hypothesis Test
I) Left-tailed take a look at if the choice speculation H1 accommodates the less-than inequality image (<), the speculation take a look at is a left-tailed take a look at.
II) Proper–tailed check: If the choice speculation H1 accommodates the greater-than inequality image (>), the speculation check is a right-tailed check.
In speculation testing, when performing a right-tailed take a look at we reject the null speculation if the take a look at statistics is bigger than the crucial worth.
Solely when the check statistic is bigger than the important worth will we be capable of rejecting the null. Often (emphasis on “often”) we hope that we will reject the null as a result of that implies that our efforts will not be in useless. In case you are testing the null speculation and you're hoping that you haven't adversely affected the method, you'll then be hoping NOT to reject the null.
III) Two–tailed check: If the choice speculation H1contains the not-equal-to image (), the speculation check is a two-tailed check. In a two-tailed check, every tail has a space of (1/2 Alpha)
Has two tails (or rejection areas) when the null speculation comprises an equal signal.
Conclusion
A statement which indicates the level of evidence (sufficient or insufficient), at what level of significance, and whether the original declare is rejected (null) or supported (alternative).
